§24.6 实数与向量相乘
1、对于非零向量
与
，下列命题是假命题的是（ ）
A．若
，则
B．若，则
C．若
，则
D．若，则
2、假如点C是线段AB的中点，那样下列结论正确的是（ ）
A．
B．
C．
D．
3、下列说法错误的是（ ）
A．假如
，那样A与B重合 B．若
,则B是OA的中点
C．若
,则 若 D．B是OA的中点则
4、
＝______，
＝______，
＝______
5、向量
与－2的方向_____
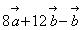6、如图，O为△ABC内一点，点D、E分别在AB、AC上，且
；若
，
，求：用向量，表示。
§24.6（2）实数与向量相乘
1、
与
的长度与方向的关系是（ ）
A.长度相等，方向相同 B. 长度相等，方向相反
C.长度不等，方向相同 D. 长度不等，方向相反
2、下列各式与是相等向量的是（ ）
A. B. 
C. D. 
3、已知
，那样的值为（ ）
A. 
B. 
C. D. 
4、计算：__________，
=___________________．
5、对于，有，请用含的式子表示
=__________
6、计算：
7、已知
，试用表示
8、和满足关系式
，用表示
9、在△ABC中，D是AB边的中点，E是BC延长线上的点，且BE=2BC，试用、
表示
§24.6 实数与向量相乘
1、下列条件不可以断定与平行的是 （ ）
A 
且
B 
C 
D
2、以下说法错误的是 （ ）
A．零向量与任一非零向量平行 B．零向量与单位向量的模不相等
C．平行向量方向相同 D．平行向量肯定是共线向量
3、若单位向量
则 = __________.
4、已知向量
方向相反，长度为6，则
5、如图，梯形ABCD中，AD∥BC，AD=3，BC=5。EF是中位线，设
,
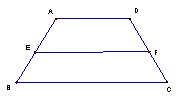则
6、化简：
（1）_____________。
（2）______________。
（3）______________。
7、如图，已知DE∥AC，DF∥AB，BD：DC=2：5，设
．
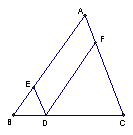
表示：
8、已知
、
都是已知向量，、
都是未知向量，且+
，,求、
§24.6 实数与向量相乘
1.答案：B
分析：向量的模相等，向量未必相等
2.答案：C
分析：与
为相反向量，所以
3.答案：C
分析：
与
的方向关系不确定
4.答案：；
；
分析： 
5.答案：相反
分析：负号代表方向相反
6.答案：
分析：∵
∴
∴DE∥BC
∴
∵
∴
§24.6（2）实数与向量相乘
1.答案：A
分析：相等向量长度相等，方向相同
2.答案：D
分析：
3.答案：C
分析：
4.答案：；
分析：；
5.答案：
分析：
，所以
6.答案：
分析：
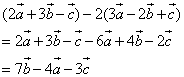
7.答案：=
分析：
=
8.答案：
分析：
，
=
=
=
=
=
9.答案：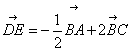
分析：
∵D是AB边的中点，BE=2BC
∴
∴
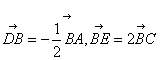
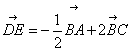
§24.6 实数与向量相乘
1.答案：D
分析：向量的模相等，向量未必相等
2.答案：C
分析：平行向量方向可能相同也会相反
3.答案：
1
分析：单位向量的模为1
4.答案：-6
分析：
5.答案：
分析：EF=4，应该注意方向相反
6.答案：
，，
分析：
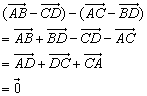
7.答案：；；；
分析：∵BD：DC=2：5
∴
∵DF∥AB
∴
∴
∵
∴
∴
8.答案：=
；
分析：+，=
